Project Euler Solution using C#: Problem 29 : Distinct powers

Problem:

Consider all integer combinations of a^b for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:

2^2=4, 2^3=8, 2^4=16, 2^5=32
3^2=9, 3^3=27, 3^4=81, 3^5=243
4^2=16, 4^3=64, 4^4=256, 4^5=1024
5^2=25, 5^3=125, 5^4=625, 5^5=3125
If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:

4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125

How many distinct terms are in the sequence generated by a^b for 2 ≤ a ≤ 100 and 2 ≤ b ≤ 100?

Solution:

static void Main(string[] args)
{
    var aMin = 2;
    var aMax = 100;

    var bMin = 2;
    var bMax = 100;

    List lst = new List();

    for (int a = aMin; a <= aMax; a++)
    {
        for (int b = bMin; b <= bMax; b++)
        {
            lst.Add(Math.Pow(a, b));
        }
    }

    var distinctRslt = lst.Distinct().ToList();
    distinctRslt.Sort();

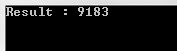
    Console.WriteLine("Result : " + distinctRslt.Count());
    Console.ReadLine();
}

Output :